從圖3同樣可以看出,長方形玻璃板,隨著孔心邊距的增大,玻璃板中心和板邊中心的位移也呈現(xiàn)迅速下降的趨勢。為了控制玻璃板的變形,同時也需要考慮孔心邊距對孔邊緣集中應力的影響,我們研究發(fā)現(xiàn),比較合理的孔心邊距是100mm。
(3)正方形玻璃板變形隨玻璃厚度的變化(見圖4孔心邊距為100~),其邊長分別為2、1.8、1.5、1.2舫擒厚詹為6、8、10、12、15mm。
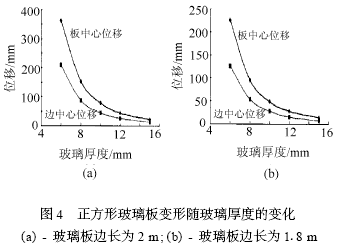
從圖4中可以看出,正方形玻璃板,隨著玻璃板厚度的增大,玻璃板中心和板邊中心的位移也呈現(xiàn)迅速下降的趨勢。
(4)長方形玻璃板變形隨玻璃厚度的變化(見圖5)孔心邊距為l00 mm,計算模型共4組,其邊長分別為2mXl.8m、2m Xl.5m、2mXl.2m、2 m X1m破璃厚度為6、8、10、12、15mm。考慮孔的影響,孔徑為36mm。
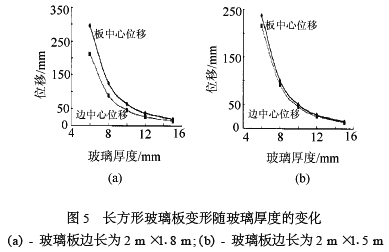
從圖5同樣可以看出,長方形玻璃板,隨著玻璃板厚度的增大,玻璃板中心和板邊中心的位移也呈現(xiàn)迅速下降的趨勢。
通過以上計算可以看出:
(1)對于目前通用的長方形和正方形玻璃板,隨著支承點孔心邊距的增大玻璃板中心和玻璃板板邊中心的位移減小。這主要是因為孔心邊距的不斷增大,外圍玻璃板受力的反翹作用使得玻璃板中心和玻璃板邊緣處的應力減少位移得到控制。
(2)當玻璃板的尺寸和玻璃孔心邊距相同時,隨著玻璃厚度的增大玻璃板中心和邊緣中心處的位移不斷減小。這是因為厚度的增加便得玻璃板抵抗垂直于平面的
彎曲能力加強,從而玻璃板邊緣和中心的位移變小。
4、點式連接玻璃板變形性能的試驗結(jié)果比較分析
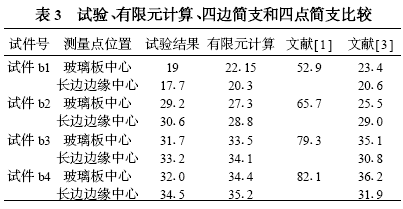
為研究點式玻璃的承載性能我們進行了1:1模型加載試驗t9,將試件按bl、b2、b3、b4編號。試驗模型采用實際工程的同批試件尺寸為1.260m X0.890m-1.36m X0.9m荷載為均布考慮孔的影響孔徑為36 mm,厚度為12mm。為了便于比較我們按試件具體尺寸進行相應的有限元計算表3中還列出文獻[1]和文獻[3]計算公式的計算結(jié)果。
 上一頁1234下一頁
上一頁1234下一頁























