|
【專家檔案】
專家姓名：劉忠偉
技術(shù)職稱：教授級高級工程師，工學(xué)博士
技術(shù)職務(wù)：主任
專長：建筑玻璃應(yīng)用科學(xué)與技術(shù)、建筑物理、建筑節(jié)能、建筑幕墻、門窗等專業(yè)的設(shè)計與研究。
從事專業(yè): 1.建筑幕墻設(shè)計與計算。 2.建筑幕墻應(yīng)用技術(shù)咨詢；《建筑玻璃應(yīng)用技術(shù)規(guī)程》JGJ113主編。<<<<專家詳細資料及論文集 |
1.前言
建筑玻璃在風(fēng)荷載作用下是典型的薄板彎曲問題，薄板在垂直荷載作用下的彎曲同題在彈性力學(xué)中有解析解，可準確計算薄板中最大彎曲應(yīng)力和位置以及最大撓度和位置。但彈性力學(xué)解決薄板彎曲問題的基本假設(shè)之一是薄板的最大撓度不超過板厚的三分之一，建筑玻璃厚度一般為4m一15mm之間，在彈性力學(xué)范圍內(nèi)允許的玻璃撓度變形一般為lmm一5mm，而實際上玻璃在風(fēng)荷載作用下的撓度變形一般可達幾十毫米，甚至上百毫米，已遠遠超出彈性力學(xué)的適用范圍，繼續(xù)采用彈性力學(xué)的方法計算出的結(jié)果過于保守，原因是其幾何非線性必須加以考慮。目前在日本和澳大利亞采用一種半理論、半經(jīng)驗的計算公式，經(jīng)試驗驗證，計算結(jié)果與實驗結(jié)果比較符合。日本的公式:
在公式(1)、(2)和(3)中，對于任何長寬比的矩形玻璃，都采用同一面積，這里存在著誤差，因為同等面積條件下，不同長寬比的矩形玻璃，其
承載力是不同的。對于
平板玻璃、
半鋼化玻璃和
鋼化玻璃.僅采用抗
風(fēng)壓調(diào)整系數(shù)處理也存在著誤差，因為這三種玻璃沿玻璃
斷面的
內(nèi)應(yīng)力分布是不同的，因此其承載力也不同。由于玻璃在風(fēng)荷載作用下的
力學(xué)性能研究試驗量巨大，耗時長，因此各國在當時基本上都是采用類似的計算方法，我國的工程行業(yè)標準《建筑玻璃應(yīng)用技術(shù)規(guī)程》
JGJ113-2003也采了這種方法，基本能滿足設(shè)計要求。
澳大利亞國家標準AS1288 2006版中采用了新的方法，考慮了矩形玻璃長寬比的影響，將原來計算
玻璃板面積，改為計算不同長寬比條件下的最大跨度。考慮了不同種類玻璃的各自特性，對
平板玻璃、半鋼化玻璃和鋼化玻璃分別采用不同的計算參數(shù)。
中空玻璃由原來兩片玻璃同時考慮，改為按荷載分配系數(shù)各自獨立計算，同時增加了玻璃板撓度限值計算方法，其精確度比1989版的更高、更合理、更全面，本文在此介紹這種新方法。
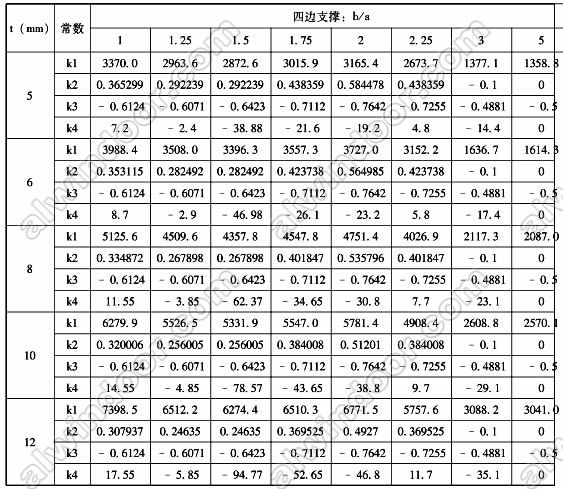
2.玻璃承載力極限狀態(tài)計算
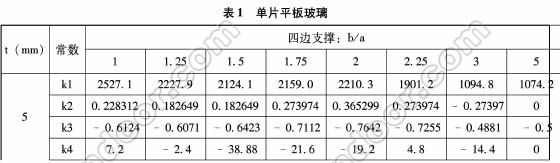
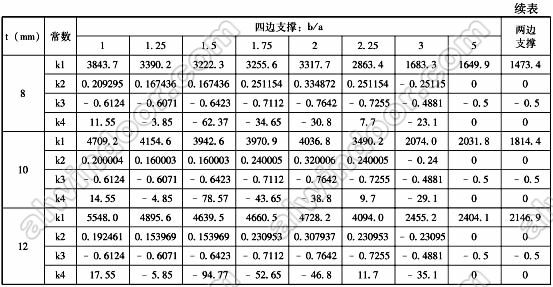
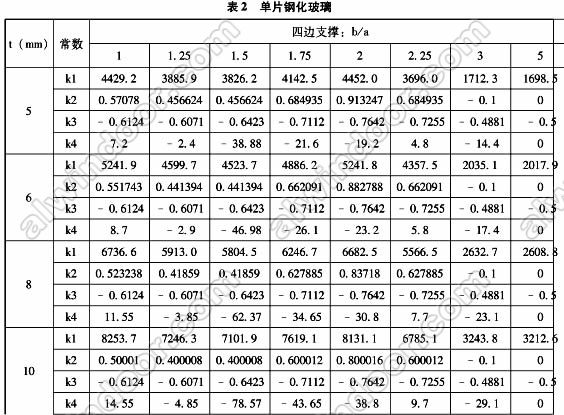
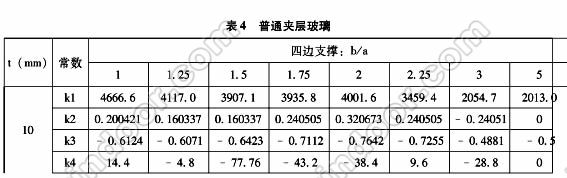
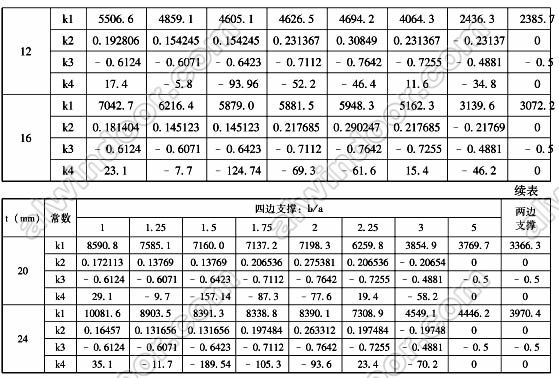
表3 半單片鋼化玻璃
上一頁12下一頁
